DGGS

Discrete Grids

The Discrete Global Grid System (DGGS), as the name implies, is a discrete grid, and to understand DGGS, we need to understand it's baseline and it's advantages. There are a number of discrete global grids, the one used here is called graticules. The graticules are cells bounded by segments, that divide Earth’s surface by degrees of longitude and latitude. When looking at the globe, looking closely towards the poles the individual cells become smaller, showing a distortion. Those types of global grids are not practical to index, store or process spatial data, the only way to index is to project this grid into a 2D plane, therefore, creating rectangular grids that we called raster. Its very hard to consider these types of grid for a 3D environment.

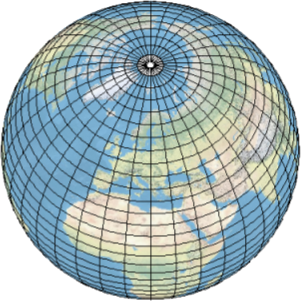
Hence comes the DGGS. This approach can be implemented using a so called Discrete Global Grid System (DGGS).

The usefulness of DGGS

The Open Geospatial Consortium (OGC) DGS working group has formalized a standard, the OGC/ISO DGGS Abstract Specification (2017) that defines: “A Discrete Global Grid System is a spatial reference system that uses a hierarchical tessellation of cells to partition and address the globe.” It is basically a multi-scale grid that covers the entire planet with a set of hierarchical, congruent regular cells (tessellation) of almost equal size. It can be expanded into 3D and indexed over time. It can come with different shapes, shuch as hexagons, squares, and triangles.

In our case, We are using hexagonal approach, and the DGGS cells require a unique identifier (GID), therefore, we use a powerful hierarchical indexing system called Z3, and besides that each DGGS cell stores information about the region each encompasses.